We study the concept of distance formula and the distance between two points in the chapter on coordinate geometry. The distance formula gives us the distance between a given number of points. The distance formula is derived with the help of the Pythagoras theorem in a two-dimensional space. This formula can also be extended to derive the distance between two points in a three-dimensional space. In coordinate geometry, we can find various types of distance formulas. In this article, we will discuss the concepts ofthe distance formulaand the distance between two points. We will also learn about the various applications of the distance formula so that you can understand the why behind the what of this important topic.
What Do You Mean by Distance Between Two Points?
In coordinate geometry, the length segment that joins any two given points is known as the distance between two points. An important thing that needs to be understood is that the distance between any two given points is positive in nature. We can find out the distance between two pointswith the help of the distance formula. To find out the distance between two points in a two-dimensional plane, we apply the two-dimensional distance formula. Likewise, to find out the distance between two points in a three-dimensional plane, we apply the three-dimensional distance formula.
What Do You Mean by Distance Formula?
In coordinate geometry, we have various types of distance formulas. Each of these formulas is used and applied in a particular situation. Let us now discuss the formulas for the distance between two points in a two-dimensional plane and a three-dimensional plane.
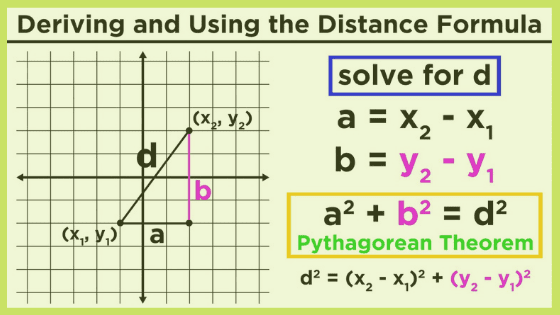
- Distance Between Two Points in a Two-dimensional Plane: This formula is also popularly known as the Euclidean distance formula. The Euclidean distance formula is given as follows:
d = √[(x2 – x1) (x2 – x1) + (y2 – y1) (y2 – y1)]
- Distance Between Two Points in a Three-dimensional Plane: Along with the x and the y coordinates, the z coordinate is also present when we discuss the three-dimensional plane. The formula of the distance between two points in a three-dimensional plane is given below:
d = √[(x2 – x1) (x2 – x1) + (y2 – y1) (y2 – y1) + (z2 – z1) (z2 – z1)]
Various Applications of Distance Formula
Distance formula can be used in various other topics of mathematics other than coordinate geometry. We have various uses of this topic in real life too which are as follows:
- It can be used to find out the distance of any given point from the origin.
- We use the distance formula to obtain the magnitude of a complex number.
- We use the distance formula to find out the distance between any two given points in a three-dimensional plane. We can also find the distance between any two given points in n-dimensional planes.
- To find out the magnitude of any given vector, we need the magnitude formula. The magnitude formula can be derived using the distance formula.
- We can find the distance between any two given points in any given water body like sea or ocean by identifying the geographic coordinates of the two given points and then by applying the distance formula.
Some Important Points Related to Distance Formula
- The length segment which is calculated with the help of the distance formula always takes a positive sign.
- The distance which is obtained using the distance formula is the shortest linear distance between any two given points.
- An interesting thing to note about the distance formula is that it gives the same answer for the points which can be located in any of the four quadrants.
If you want to learn more about the concepts of distance formula and its applications in a detailed, fun, and interesting manner, visit Cuemath to learn from the best teachers of the subject.